Newton Rapshon

Método de Newton Rapshon

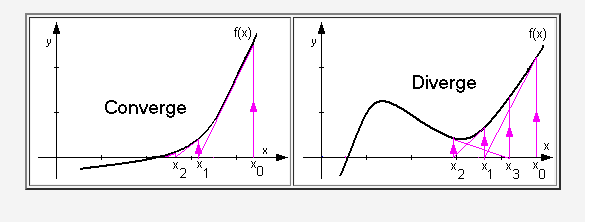
El método de Newton-Raphson es un método de segundo orden para encontrar raíces de una función \(f(x)\), es decir, encontrar \(x\) tal que \(f(x)=0\). Para obtener el algoritmo del método vamos a usar el desarrollo de Taylor de \(f(x)\) alrededor de \(x_0\):

\[f(x) = f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)}{2!}(x-x_0)^2 + \frac{f'''(x_0)}{3!}(x-x_0)^3 + \cdots\] truncando la serie a primer orden y despejando \(x\) obtenemos: \[0=f(x_0) + f'(x_0)(x-x_0)+O(|x-x_0|^2)\] Note que aquí podemos construir una función \[g(x) = f(x_0) + f'(x_0)(x-x_0)\] que pasa por el punto \((x_0,f(x_0))\) y tiene pendiente \(f'(x_0)\), es decir, es la recta tangente a \(f(x)\) en \(x_0\), de esta forma podemos definir \(x_1\) como la intersección de \(g(x)\) con el eje \(x\), de donde \[x_1 = x_0 - \frac{f(x_0)}{f'(x_0)}\] de forma iterativa tenemos el método de Newton-Raphson:

\[x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\]

Note que el método de Newton-Raphson es un método de segundo orden, es decir, el error en la aproximación \(x_n\) es proporcional al cuadrado del error en la aproximación \(x_{n-1}\).

Note que el método de Newton-Raphson requiere el cálculo de la derivada de \(f(x)\), en algunos casos esto puede ser complicado, en estos casos se puede usar el método de la secante que es una aproximación numérica de la derivada.

Note que el método de Newton-Raphson puede no converger, en estos casos se puede usar el método de la bisección.

Note que el algoritmo necesita un punto inicial \(x_0\) cercano a la raíz que se quiere encontrar.

Ejercicio Escriba cuales son las ventajas y desventajas del método de Newton Raphson sobre el método de la bisección.

## newton rapson method
import numpy as np
import matplotlib.pyplot as plt
import math
def f(x):
    return x**3-2*x-5
def df(x):
    return 3*x**2-2
def newton(x0,eps):
    x1=x0-f(x0)/df(x0)
    while abs(x1-x0)>eps:
        x0=x1
        x1=x0-f(x0)/df(x0)
    return x1

Ejercicio Note que el algoritmo anterior tiene un problema. ¿Cuál es? ¿Cómo lo solucionaría?

Reescriba el algoritmo anterior para que no tenga el problema que identificó.

Note que en este método tenemos que calcular la derivada, lo podemos hacer de dos formas:

Escribir deiractamente la derivada de la función.
Utilizar la función Derivative de SymPy y luego evaluarla en el punto.

En el siguiente código usted vera como se puede usar la función Derivative de SymPy para calcular la derivada de una función y luego evaluarla en un punto.

import sympy as sp
import numpy as np
import matplotlib.pyplot as plt

# Definir la variable simbólica
x = sp.symbols('x')

# Definir la función simbólica
funcion_simbolica = x**2 + 3*x + 2
# Función numpy
funcion_numpy = sp.lambdify(x, funcion_simbolica, 'numpy')

# Calcular la derivada
derivada_simbolica = sp.diff(funcion_simbolica, x)

# Convertir la derivada en una función de NumPy
derivada_numpy = sp.lambdify(x, derivada_simbolica, 'numpy')

# Crear un rango de valores para x
x_vals = np.linspace(-10, 10, 400)

# Calcular los valores correspondientes para la función y su derivada
funcion_vals = funcion_numpy(x_vals)
derivada_vals = derivada_numpy(x_vals)


# Crear una figura y ejes
plt.figure(figsize=(10, 6))
plt.title('Función y su Derivada')
plt.xlabel('x')
plt.ylabel('y')

# Graficar la función original
plt.plot(x_vals, funcion_vals, label='Función Original')

# Graficar la derivada
plt.plot(x_vals, derivada_vals, label='Derivada')

# Mostrar leyenda
plt.legend()

# Mostrar el gráfico
plt.grid()
plt.show()

Ejercicio Use el anterior código para reformar el método de Newton-Raphson para que solo se necesite la función \(f\) y el internamente se calcule la derivada simbólica.

librerías externas

Existen diferentes librerías para calcular encontrar la raíz de una función, en este caso se usará la librería de scipy, la cual contiene una función llamada newton que permite encontrar la raíz de una función, para esto se debe ingresar la función, la derivada de la función y el valor inicial de la raíz. en el siguiente enlace encontraras las funciones que contiene la librería de scipy.

Ejercicio + Lea atentamente la documentación y haga un resumen de lo encontrado. + Encuentre la raíz de la función \(f(x)=x^3-2x^2-5\), usando los métodos de bisección y newton (su implementación, y el de la librería scipy ), compare los resultados obtenidos, aproximación, tiempo de computo, número de iteraciones, etc.

Para elvaluar el tiempo de computo usted puede usar el siguiente código:

```python
import time
# Registro del tiempo de inicio
start_time = time.time()

# Código de tu algoritmo
# ...

# Registro del tiempo de finalización
end_time = time.time()

# Cálculo del tiempo de ejecución
execution_time = end_time - start_time

print("Tiempo de ejecución:", execution_time, "segundos")
```