Operaciones en \(\mathbb{R}^2\)

Clase de Álgebra Lineal: Operaciones en \(\mathbb{R}^2\)

En esta clase, vamos a repasar los conceptos fundamentales de los vectores en \(\mathbb{R}^2\), la suma de vectores, la multiplicación por escalar, las normas y la proyección de un vector sobre otro.

Vectores en \(\mathbb{R}^2\)

Definición

Un vector en \(\mathbb{R}^2\) es un par ordenado de números reales.
Podemos denotarlo como \(\mathbf{v}=(v_1,v_2)\) o como columna: \[ \mathbf{v}=\begin{pmatrix}v_1\\v_2\end{pmatrix} \] donde \(v_1,v_2\in\mathbb{R}\).

Interpretación Geométrica

Cada vector en \(\mathbb{R}^2\) puede representarse como un segmento dirigido en el plano cartesiano, con origen en \((0,0)\) y extremo en \((v_1,v_2)\).
Su longitud (o magnitud) y dirección permiten describir el vector de forma geométrica.

Suma de Vectores

Definición de la Suma

Dadas dos vectores \(\mathbf{u}=(u_1,u_2)\) y \(\mathbf{v}=(v_1,v_2)\) en \(\mathbb{R}^2\), su suma se define como: \[ \mathbf{u}+\mathbf{v}=(u_1+v_1,u_2+v_2) \]

Interpretación Geométrica

Para sumar los vectores \(\mathbf{u}\) y \(\mathbf{v}\) en el plano, se utiliza la regla del paralelogramo o el método cabeza-cola:
1. Trasladar (sin rotar) el vector \(\mathbf{v}\) de modo que su cola coincida con la cabeza de \(\mathbf{u}\).
2. El vector resultante va desde la cola de \(\mathbf{u}\) hasta la cabeza de \(\mathbf{v}\).

Ejemplo

Supongamos: \[ \mathbf{u}=(2,3),\mathbf{v}=(-1,5). \] Entonces: \[ \mathbf{u}+\mathbf{v}=(2+(-1),3+5)=(1,8). \]

Multiplicación por un Escalar

Definición

Dado un vector \(\mathbf{v}=(v_1,v_2)\) y un número real \(\alpha\in\mathbb{R}\) (llamado escalar), la multiplicación por escalar se define como: \[ \alpha\mathbf{v}=(\alpha v_1,\alpha v_2) \]

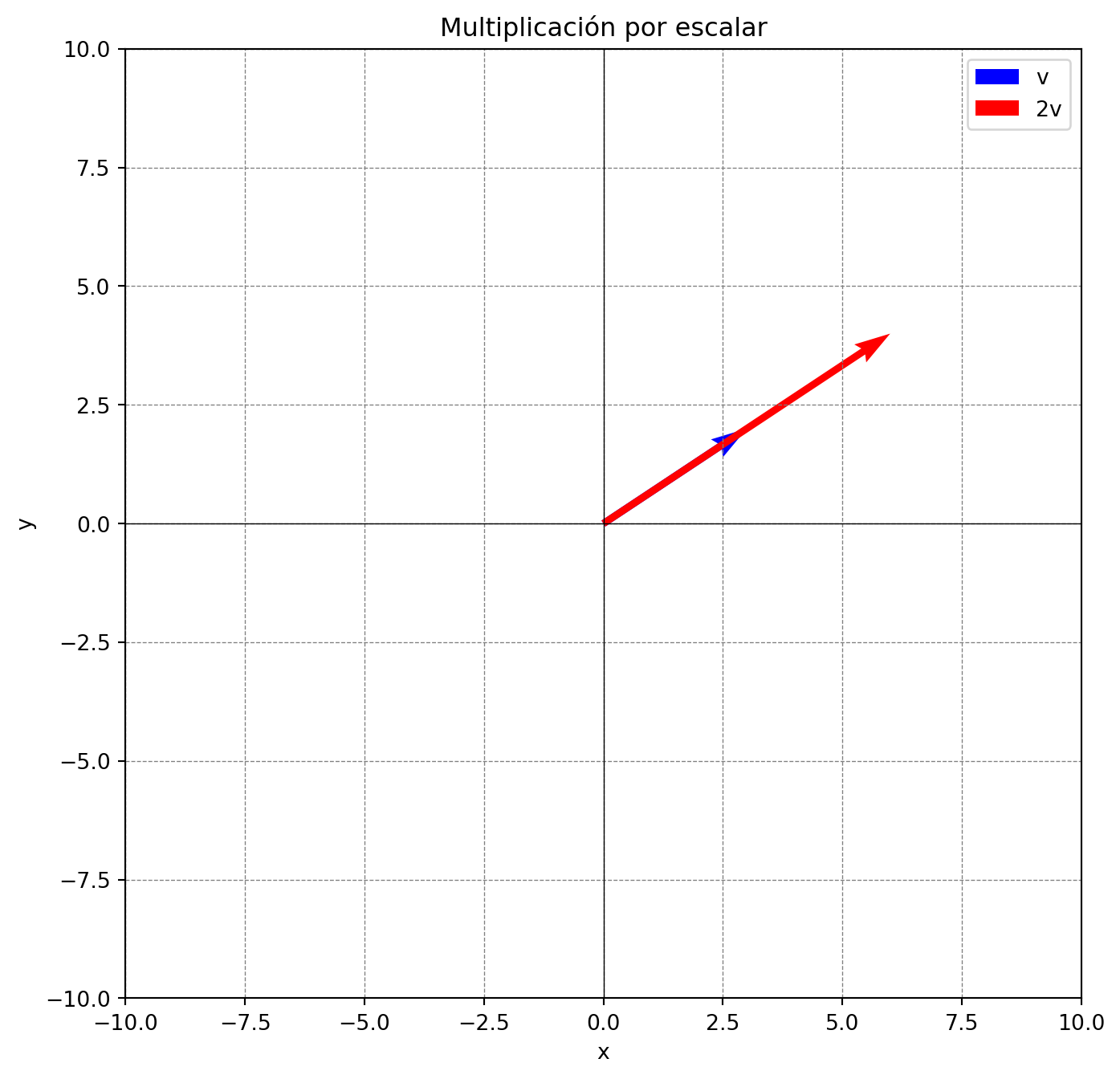
Interpretación Geométrica

Multiplicar un vector por un escalar estira o encoge al vector (cambiando su magnitud) y, si \(\alpha<0\), también invierte su dirección.

Ejemplo

Sea \(\mathbf{v}=(2,-1)\) y \(\alpha=3\). Entonces: \[ 3\mathbf{v}=3\cdot(2,-1)=(6,-3). \]

Propiedades de la Suma y la Multiplicación por Escalar en \(\mathbb{R}^2\)

Las operaciones de suma de vectores y multiplicación por escalar en \(\mathbb{R}^2\) cumplen con las siguientes propiedades:

Conmutatividad de la Suma: \[ \mathbf{u}+\mathbf{v}=\mathbf{v}+\mathbf{u}. \]
Asociatividad de la Suma: \[ (\mathbf{u}+\mathbf{v})+\mathbf{w}=\mathbf{u}+(\mathbf{v}+\mathbf{w}). \]
Elemento Neutro de la Suma: \[ \mathbf{v}+\mathbf{0}=\mathbf{v}, \] donde \(\mathbf{0}=(0,0)\) es el vector nulo.
Inverso Aditivo: \[ \mathbf{v}+(-\mathbf{v})=\mathbf{0}. \]
Distributividad de la Multiplicación por Escalar: \[ \alpha(\mathbf{u}+\mathbf{v})=\alpha\mathbf{u}+\alpha\mathbf{v}. \]
Asociatividad de la Multiplicación por Escalar: \[ \alpha(\beta\mathbf{v})=(\alpha\beta)\mathbf{v}. \]
Identidad de la Multiplicación por Escalar: \[ 1\mathbf{v}=\mathbf{v}. \]

Normas de un Vector

La norma de un vector se refiere a la “longitud” o “magnitud” de dicho vector. Existen varias normas, pero la más común en \(\mathbb{R}^2\) es la norma Euclidiana.

Norma Euclidiana (\(\|\cdot\|_2\)), llamada norma \(L_2\)

Para un vector \(\mathbf{v}=(v_1,v_2)\), la norma euclidiana se define como: \[ \|\mathbf{v}\|_2=\sqrt{v_1^2+v_2^2}. \] - Ejemplo: Si \(\mathbf{v}=(3,4)\), \[ \|\mathbf{v}\|_2=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5. \]

Otras Normas (opcional)

Norma 1: \(\|\mathbf{v}\|_1=|v_1|+|v_2|\).
Norma Infinito: \(\|\mathbf{v}\|_\infty=\max(|v_1|,|v_2|)\).

Para la mayor parte de los casos en geometría básica y proyecciones, la norma euclidiana es la más utilizada.

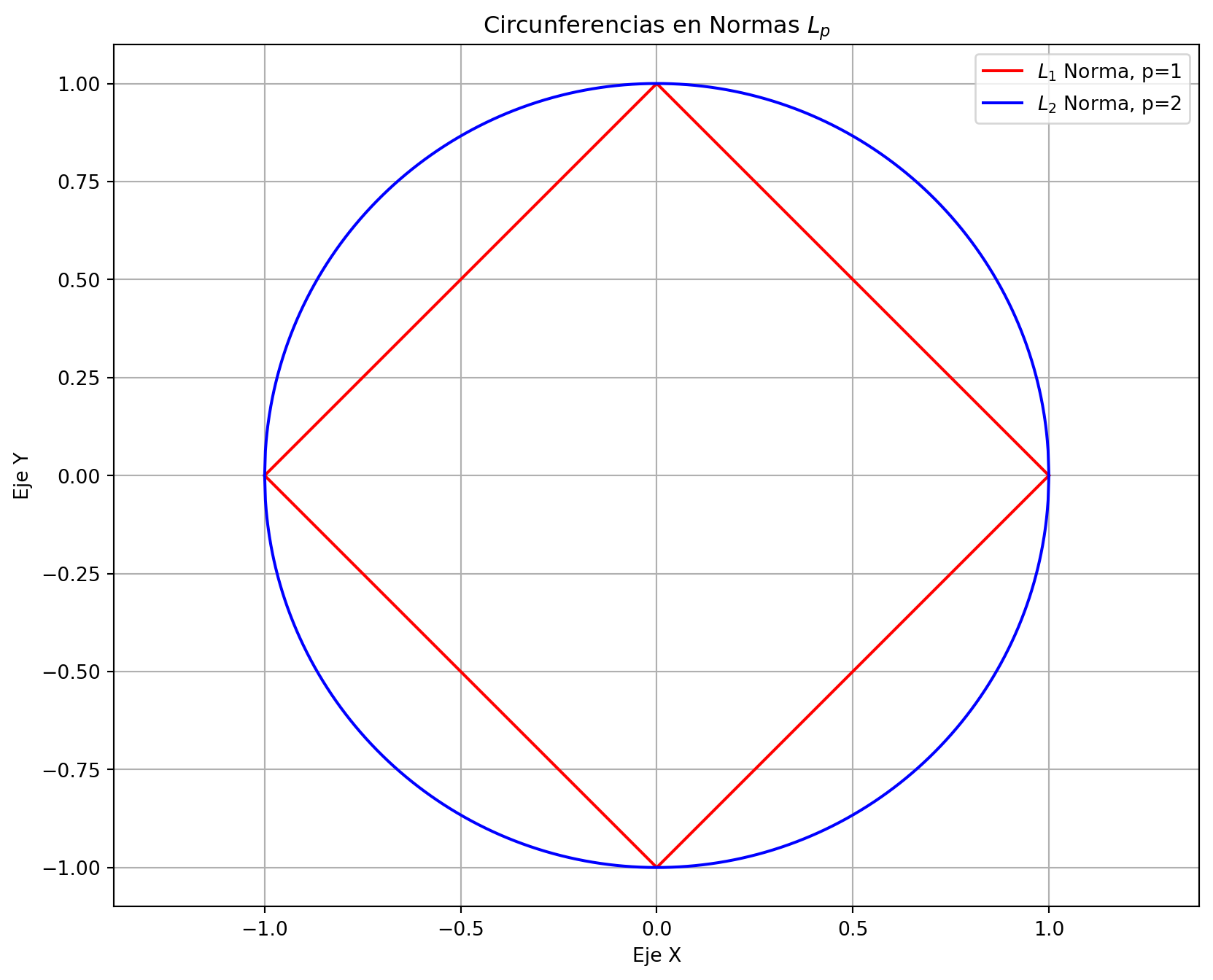
De esta forma podemos visualizar las diferencias entre las normas de un vector en \(\mathbb{R}^2\). Para ello veremos como se puede interpretar una circunferencia en cada una de las normas.

Ejercicio

¿Cómo se debería dibujar la circunferencia en el caso de la norma infinito?

Propiedades de la Norma

La norma euclidiana en \(\mathbb{R}^2\) cumple con las siguientes propiedades:

Positividad: \[ \|\mathbf{v}\|_2\geq 0,\quad\text{y}\quad\|\mathbf{v}\|_2=0\text{ si y solo si }\mathbf{v}=\mathbf{0}. \]
Homogeneidad: \[ \|\alpha\mathbf{v}\|_2=|\alpha|\|\mathbf{v}\|_2. \]
Desigualdad Triangular: \[ \|\mathbf{u}+\mathbf{v}\|_2\leq\|\mathbf{u}\|_2+\|\mathbf{v}\|_2. \]

Proyección de un Vector en \(\mathbb{R}^2\)

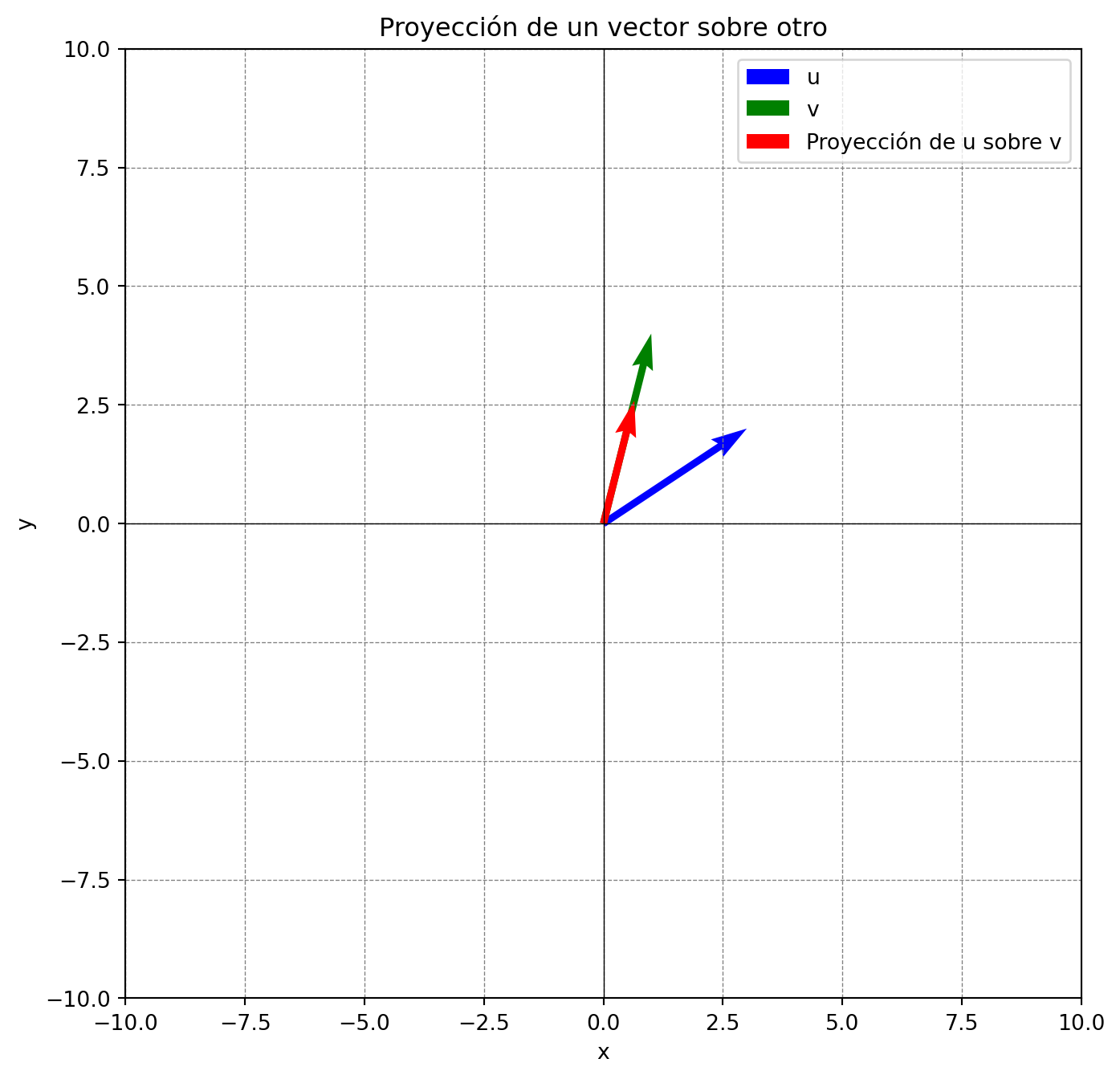
La proyección de un vector \(\mathbf{u}\) sobre otro vector \(\mathbf{v}\) (asumiendo \(\mathbf{v}\neq\mathbf{0}\)) es el vector en la dirección de \(\mathbf{v}\) que representa la parte de \(\mathbf{u}\) en esa dirección.

5.1 Definición

La proyección de \(\mathbf{u}\) sobre \(\mathbf{v}\), denotada como \(\text{proj}_{\mathbf{v}}(\mathbf{u})\), se define como: \[ \text{proj}_{\mathbf{v}}(\mathbf{u})=\left(\frac{\mathbf{u}\cdot\mathbf{v}}{\mathbf{v}\cdot\mathbf{v}}\right)\mathbf{v}. \] - \(\mathbf{u}\cdot\mathbf{v}\) es el producto punto: \[ \mathbf{u}\cdot\mathbf{v}=u_1v_1+u_2v_2. \] - \(\mathbf{v}\cdot\mathbf{v}=\|\mathbf{v}\|_2^2=v_1^2+v_2^2\).

5.2 Ejemplo

Sean: \[ \mathbf{u}=(2,1),\mathbf{v}=(3,0). \] 1. Calcular el producto punto \(\mathbf{u}\cdot\mathbf{v}\): \[ \mathbf{u}\cdot\mathbf{v}=(2)(3)+(1)(0)=6. \] 2. Calcular \(\mathbf{v}\cdot\mathbf{v}\): \[ \mathbf{v}\cdot\mathbf{v}=(3)(3)+(0)(0)=9. \] 3. Hallar la proyección: \[ \text{proj}_{\mathbf{v}}(\mathbf{u})=\left(\frac{6}{9}\right)(3,0)=\left(\frac{2}{3}\right)(3,0)=(2,0). \]

Geométricamente, \(\mathbf{u}\) se proyecta sobre \(\mathbf{v}\) y el vector resultante es paralelo a \(\mathbf{v}\).

6. Resumen

Vectores en \(\mathbb{R}^2\): Se representan como pares ordenados \((v_1,v_2)\).
Suma de Vectores: Suma componente a componente.
Multiplicación por Escalar: Escala la magnitud del vector y puede invertir su dirección (si el escalar es negativo).
Normas: Principalmente la norma euclidiana \(\sqrt{v_1^2+v_2^2}\) para medir la “longitud” del vector.
Proyección: \(\text{proj}_{\mathbf{v}}(\mathbf{u})\) calcula la componente de \(\mathbf{u}\) en la dirección de \(\mathbf{v}\).

Con estos conceptos, ya tienes las bases para entender y trabajar con operaciones vectoriales fundamentales en \(\mathbb{R}^2\). ¡Sigue practicando con ejemplos para reforzar tu comprensión!

Vector u: [3 2]
Vector v: [1 4]
Suma de vectores u + v: [4 6]
Vector u multiplicado por 2: [6 4]
Norma del vector u: 3.605551275463989
Proyección de u sobre v: [0.64705882 2.58823529]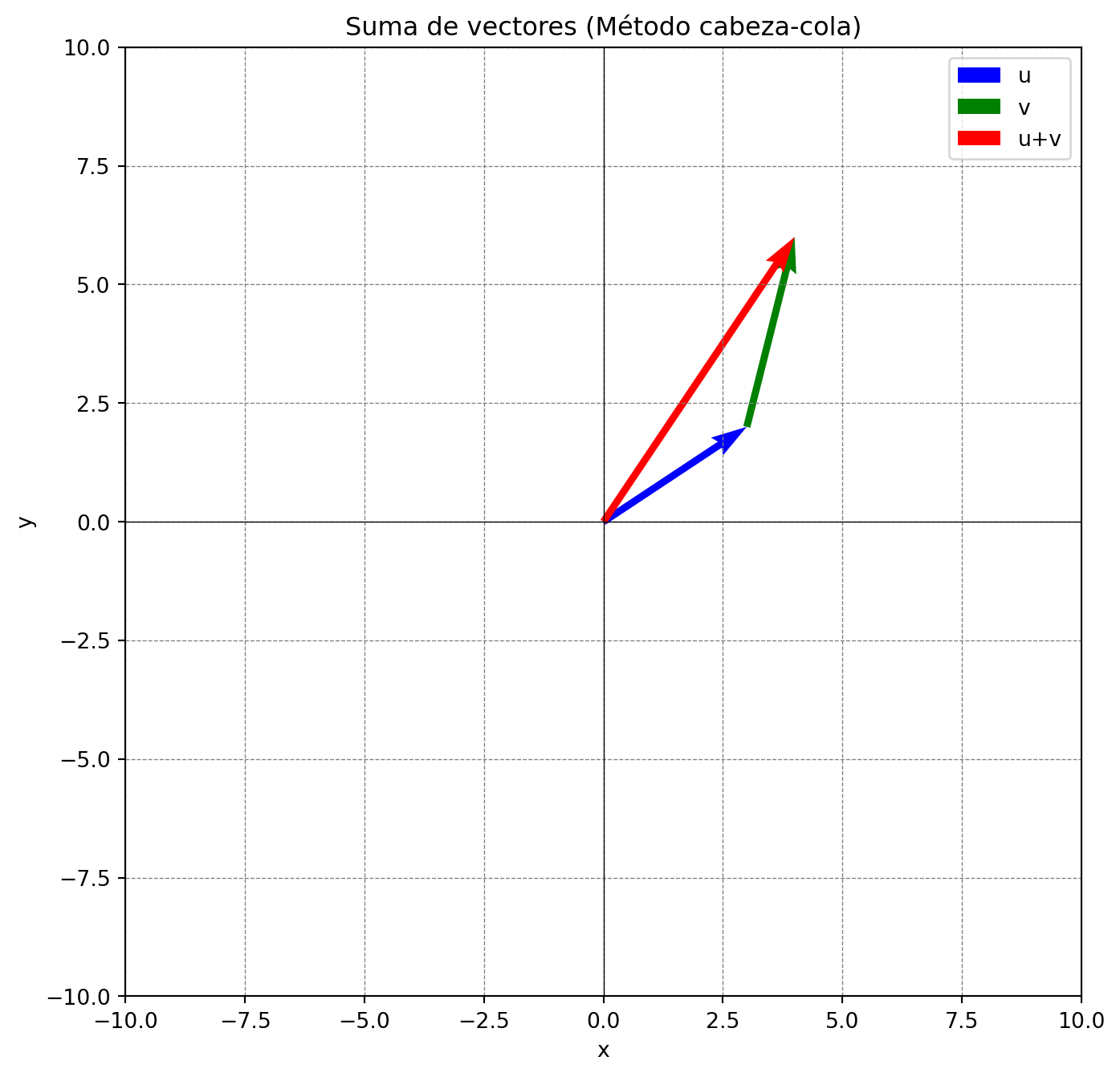

Para realizar las anteriores operaciones con vectores en \(\mathbb{R}^2\), podemos utilizar la librería NumPy en Python. A continuación, se muestra un ejemplo de código que realiza la suma de vectores, la multiplicación por escalar, el cálculo de la norma de un vector y la proyección de un vector sobre otro en \(\mathbb{R}^2\):