/home/user/miniforge3/envs/class/lib/python3.12/site-packages/IPython/core/pylabtools.py:170: UserWarning: Glyph 127968 (\N{HOUSE BUILDING}) missing from current font.
fig.canvas.print_figure(bytes_io, **kw)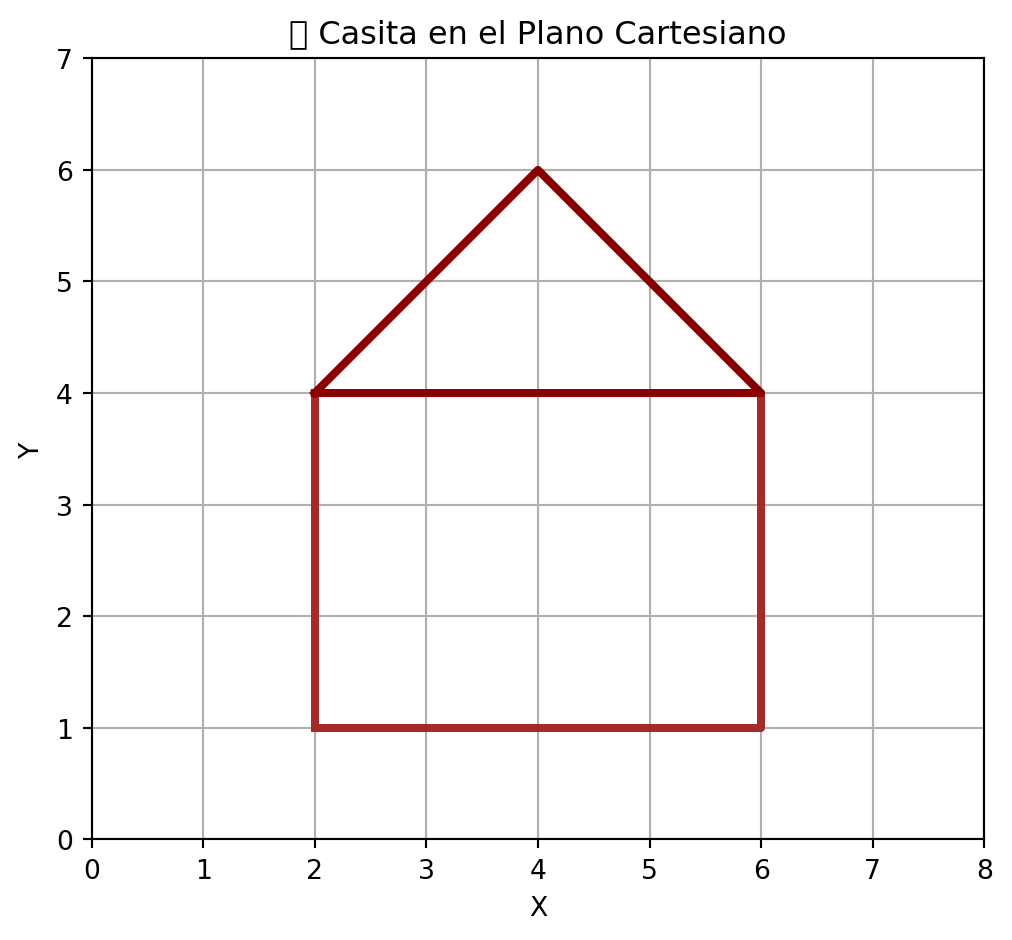
Ejercicio computacional valores y vectores propios (Matrices 2x2)
1. Matriz con Parámetros: Determina los valores propios y los vectores propios de la matriz
\[ A = \begin{bmatrix} 2 & a \\ 3 & 4 \end{bmatrix} \] en función de \(a\). Analiza los casos en los que los valores propios sean reales o complejos.
2. Matriz con Exponente: Sea la matriz
\[ B = \begin{bmatrix} 5 & -2 \\ 1 & 3 \end{bmatrix} \] Calcula sus valores propios y usa ese resultado para encontrar \(B^n\) sin multiplicaciones sucesivas.
3. Propiedades de la Suma y Producto:
\[ C = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad D = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix} \] ¿Se cumple que los valores propios de \(C+D\) son la suma de los valores propios de \(C\) y \(D\)?
4. Matriz Singular:
Encuentra una matriz no nula \(A\) con un valor propio igual a cero. Interpreta geométricamente su efecto sobre los vectores.
5. Demuestra que si \(A\) tiene valores propios \(\lambda_1, \lambda_2\), entonces:
\[ \text{traza}(A) = \lambda_1 + \lambda_2, \quad \det(A) = \lambda_1 \lambda_2. \]
6. De un ejemplo de matriz \(2 \times 2\) que no sea diagonalizable y tenga
a. 1 Valores propio real.
b. 2 Valores propios reales distintos.
c. Valores propios complejos.8. 📈 Aplicación en Economía: Modelado de Mercados Interdependientes
📌 Contexto: Evolución de Precios en Dos Sectores Económicos
En economía, los precios de bienes y servicios están interconectados. Por ejemplo, el precio de los metales afecta el costo de fabricación de automóviles, y el precio de la energía impacta la producción industrial.
Imaginemos un modelo simplificado de dos sectores económicos:
- Sector A: Producción de materias primas (metales, petróleo, insumos básicos).
- Sector B: Producción industrial (autos, electrodomésticos, maquinaria).
Cada periodo, los precios en estos sectores cambian en función de la oferta y la demanda, siguiendo la matriz de transición de precios:
\[ P_{n+1} = A P_n \]
donde \(P_n\) representa los precios en el periodo \(n\) y la matriz de influencia \(A\) es:
\[ A = \begin{bmatrix} 0.8 & 0.3 \\ 0.2 & 0.7 \end{bmatrix} \]
Cada entrada de \(A\) indica cómo el precio de un sector influye en sí mismo y en el otro sector.
- 0.8: El 80% del precio en el sector A depende de su propio precio del período anterior.
- 0.3: El 30% del precio en el sector A depende del precio del sector B del período anterior.
- 0.2: El 20% del precio en el sector B depende del precio del sector A del período anterior.
- 0.7: El 70% del precio en el sector B depende de su propio precio del período anterior.
📌 Preguntas
- ¿Cómo evolucionarán los precios en el largo plazo?
- ¿Se alcanzará un equilibrio en los precios?
- Encuentra los valores propios y vectores propios de la matriz \(A\) y explica como podrían ayudar a responder las preguntas anteriores.
- Coloca una condiciones iniciales para los precios y calcula los precios en el largo plazo.
9. 🏗️ Responde si es falso o verdadero, recuerde que el contexto A es una matriz \(2\times 2\)
Si \(A\) es una matriz simétrica, entonces sus valores propios son reales.
Si el sistema \(Ax=b\) tiene infinitas soluciones entonces \(A\) tiene un valor propio igual a cero.
Si una matriz es diagonalizable, entonces sus valores propios son reales.
Si \(A\) tiene un valor propio igual a cero, entonces \(A^{-1}\) no existe.
Si \(A\) tiene un valor propio igual a cero y otro diferente, entonces \(A\) es no es diagonalizable.
10. 🏠 Gráfica la figura que esta formada por los puntos
Observa la figura que se forma al unir los puntos en el plano cartesiano.
Esta figura se rota como se muestra en la siguiente gráfica.
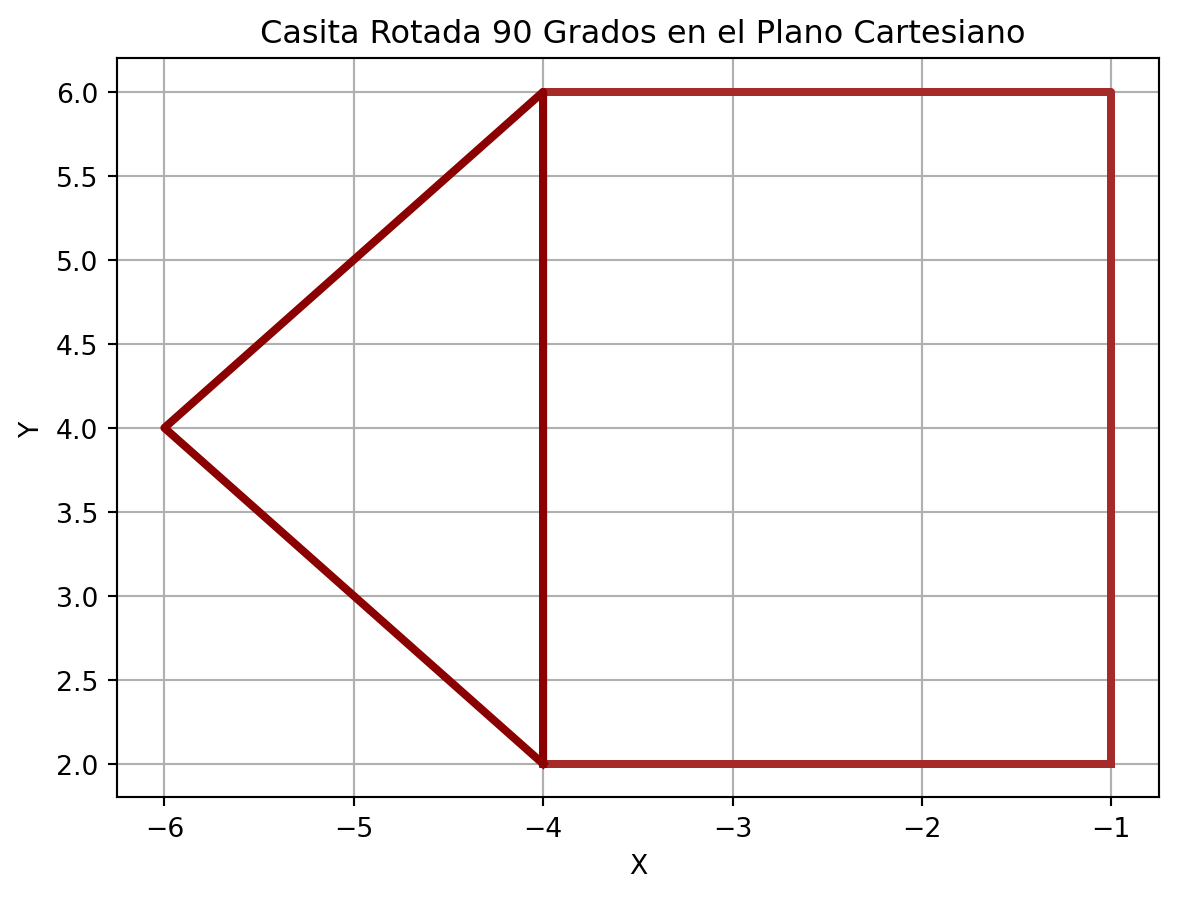
Encuentre la matriz de rotación que se utilizó para rotar la figura.