Ejercicios de Autovalores y Autovectores (Matrices 2x2)
Introducción
Ejercicios
Dada la matriz, encontrar los valores propios y vectores propios. 1. \(A = \begin{bmatrix} 4 & 2 \\ 1 & 3 \end{bmatrix}\)
\(B = \begin{bmatrix} 5 & -2 \\ 2 & 1 \end{bmatrix}\)
\(E = \begin{bmatrix} 6 & 2 \\ 2 & 3 \end{bmatrix}\)
\(G = \begin{bmatrix} -1 & -2 \\ 2 & -3 \end{bmatrix}\)
Determina para que valor \(\alpha\) la matriz \(H = \begin{bmatrix} 2 & 1 \\ 1 & \alpha \end{bmatrix}\) tiene un solo valor propio.
Un modelo lineal de evolución poblacional para dos especies está dado por la matriz:
\[ \begin{bmatrix}y_{n+1}\\ x_{n+1}\end{bmatrix}= \begin{bmatrix} 0.8 & 0.3 \\ 0.2 & 0.7 \end{bmatrix}\begin{bmatrix}y_{n}\\ x_{n}\end{bmatrix} \]
El sistema anterior, la matriz de transición describe cómo las poblaciones de dos especies (denotadas como \(y\) y \(x\)) evolucionan de un tiempo \(n\) al siguiente tiempo \(n+1\). Los elementos de la matriz representan las tasas de crecimiento y las interacciones entre las dos especies. Si la población inicial es \(y_0= 0.2\) y \(x_0=0.8\), (Usa un computador para realizar rápidamente los cálculos)
¿cuál será la población en tiempo n=10. Halla los valores propios y vectores propios para analizar el comportamiento del sistema.
Como podemos interpretar los valores propios en este contexto.
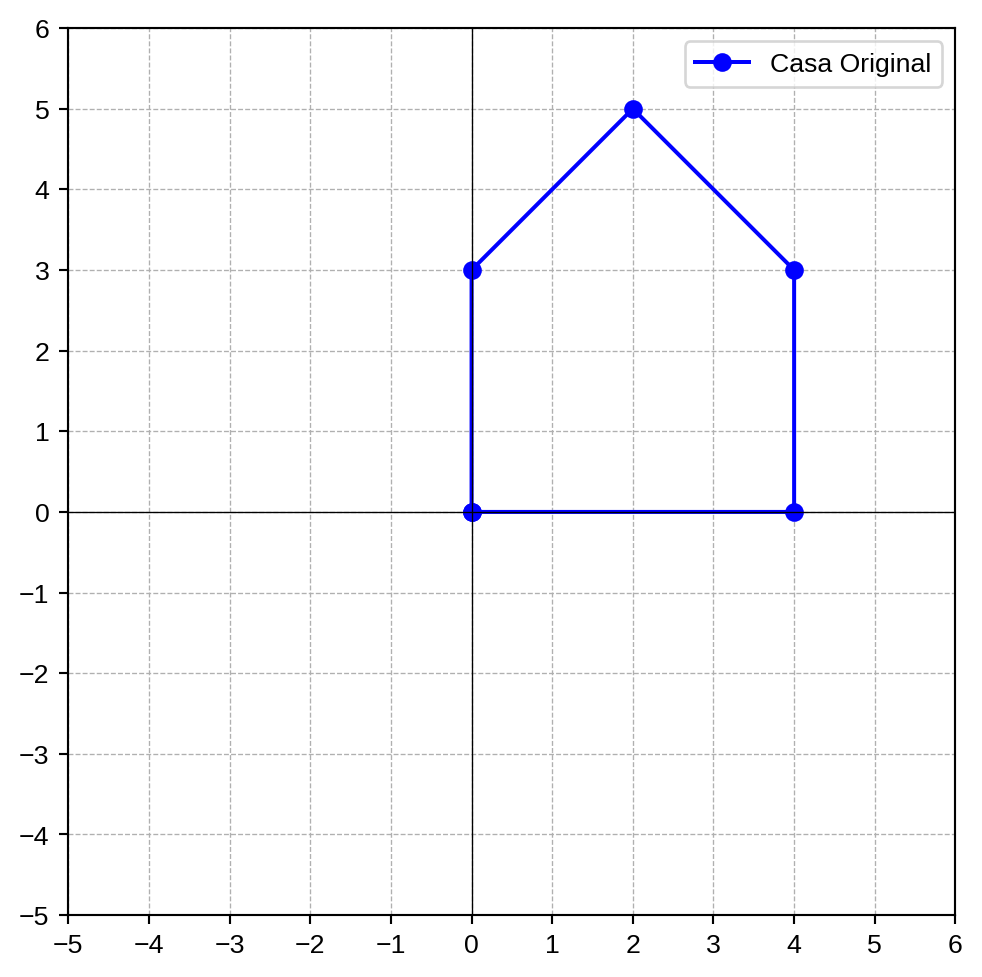
- En el siguiente plano se dibuja una casa.
Los puntos se encuentran en las coordenadas:
\[\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Punto} & A & B & C & D & E & A \\ \hline x & 0 & 4 & 4 & 2 & 0 & 0 \\ \hline y & 0 & 0 & 3 & 5 & 3 & 0 \\ \hline \end{array}\]
Multiplica a cada uno de los puntos por la matriz
\[A= \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}\]
y dibuja la nueva casa.
Como podemos interpretar la transformación de la casa en este contexto.
Encuentra los valores propios y vectores propios de la matriz de rotación y analiza su comportamiento.
¿Qué pasa si la matriz de rotación es \(A= \begin{bmatrix} 1 & 0 \\ -1 & 0 \end{bmatrix}\)? ¿Qué sucede con la casa? ¿Cuales son los valores propios y vectores propios de la matriz? ¿Qué interpretación podemos dar a los valores propios en este contexto?
Crea la matriz en python de la forma
import numpy as np H = np.array([[0, 4, 4, 2, 0, 0], [0, 0, 3, 5, 3, 0]])
A= np.array([[2, 1], [1, 2]])
para aplicar la transformación
H_transformed = A @ H
Para dibujar la nueva casa.
import matplotlib.pyplot as plt
plt.plot(H[0], H[1], ‘bo-’, label=“Casa Original”) # Dibujo original
plt.plot(H_transformed[0], H_transformed[1], ‘ro-’, label=“Casa Transformada”) # Transformada