Independencia lineal
Subespacio de \(\mathbb{R}²\)
Un subespacio de \(\mathbb{R}^2\) es un conjunto de vectores que cumple con las siguientes propiedades:
- El vector cero está en el subespacio.
- El subespacio es cerrado bajo la suma de vectores.
- El subespacio es cerrado bajo la multiplicación por un escalar.
Ejemplo
El conjunto de todos los vectores que estan contenidos en una recta que pasa por el origen es un subespacio de \(\mathbb{R}^2\). Esto se debe a que la recta cumple con las tres propiedades mencionadas anteriormente. ¿cómo podemos mostrar esto?
Ejemplo 2
El vector cero es un subespacio. ¿Por qué?
Combinación lineal
La combinación lineal es una operación entre un conjunto de vectores, por ejemplo si tenemos el conjunto de vectores \(W=\{\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3\}\) no nulos, se puede decir que un vector \(\mathbf{w}\) es una combinación lineal de los vectores de \(W\) si se puede expresar como
\[\mathbf{w} = \alpha_1 \mathbf{v}_1 + \alpha_2 \mathbf{v}_2 + \alpha_3 \mathbf{v}_3\]
donde \(\alpha_1, \alpha_2, \alpha_3\) son números reales. Ademas, el conjunto generado por todas las combinaciones lineales de los vectores de \(W\) se llama el espacio generado por \(W\) y se denota por \(Span(W)\).
Ejemplo
Vamos a estudiar el conjunto generado por el vector \(\mathbf{v} = (1, 2)\) en \(\mathbb{R}^2\). Lo primero que vamos a estudiar es el conjunto de todas las combinaciones lineales de \(\mathbf{v}\), es decir, el conjunto de todos los vectores que se pueden obtener multiplicando \(\mathbf{v}\) por un número real. Para ello vamos a graficar el vector \(\mathbf{v}\) y luego multiplicamos a este vector por un número real \(c\) y graficamos el vector resultante. Como lo vemos en la siguiente figura el conjunto de todas las combinaciones lineales de \(\mathbf{v}\) es una recta de color negro que pasa por el origen y tiene dirección \(\mathbf{v}\).
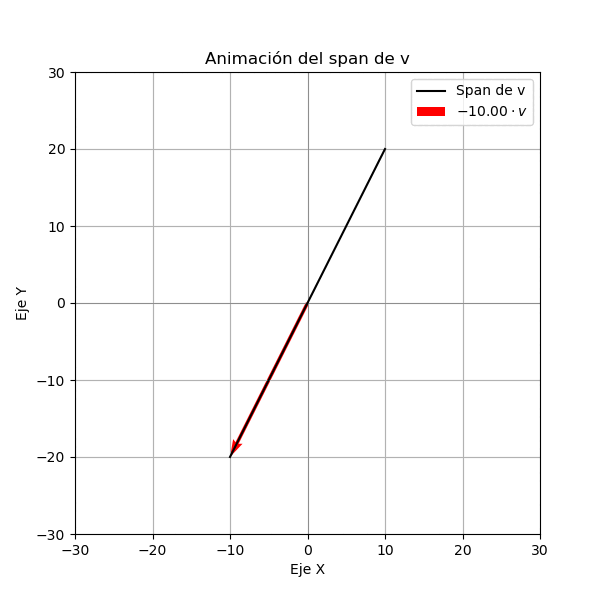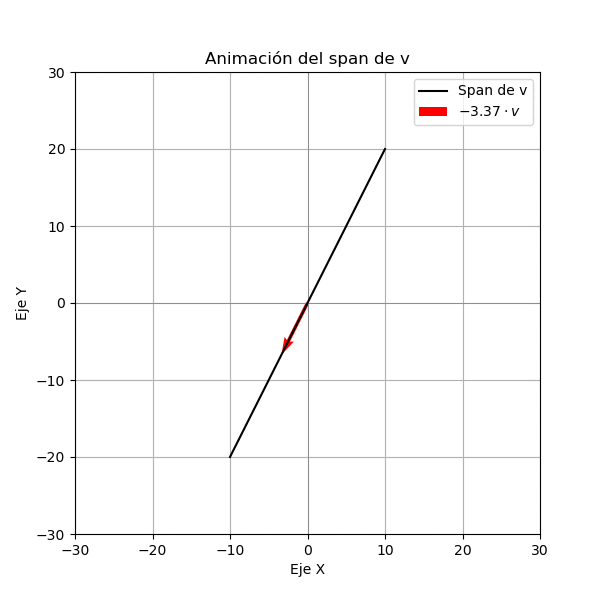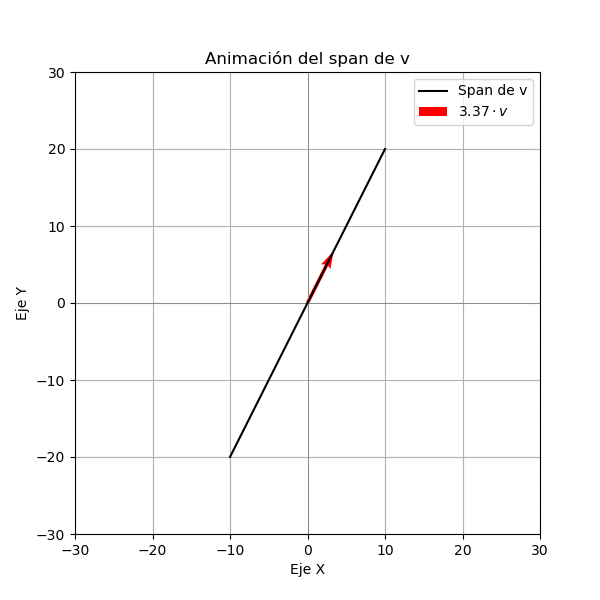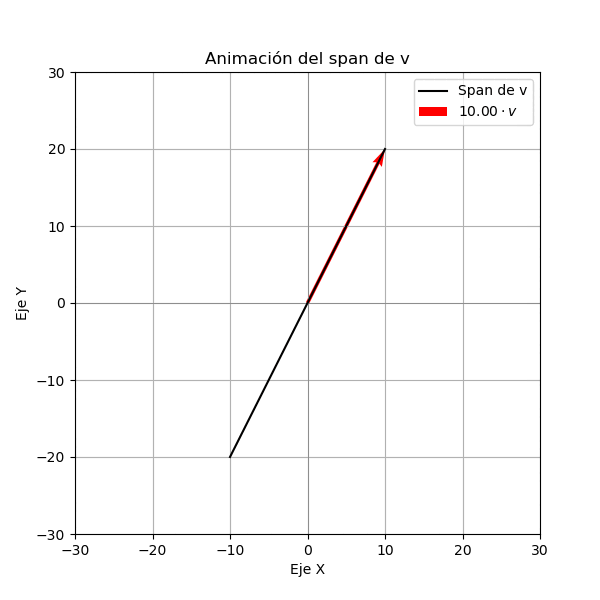
Ejemplo 2
Vamos a estudiar si el vector \(\mathbf{w} = (10, 5)\) es una combinación lineal del vector \(\mathbf{v}_1 = (1, 2)\), Note que el vector
\[\mathbf{w} = 5 \mathbf{v}_1\] puesto que
\[5 \mathbf{v}_1 = 5(1, 2) = (5, 10)\]
De esta forma podemos decir que \(\mathbf{w}\) es una combinación lineal de \(\mathbf{v}_1\). Además podemos ver que \(\mathbf{w}\in Span(\mathbf{v}_1)\).
Aquí nos surgen varias preguntas que gráficamente podríamos resolver como
¿Si \(\mathbf{w},\mathbf{v}_1\) son paralelos y vectores de \(\mathbb{R}^2\), estos formaran el mismo espacio generado?
¿El vector \(\mathbf{z}=(5,2)\) también es una combinación lineal de \(\mathbf{v}_1=(1,2)\)?
Ahora supongamos que tenemos dos vectores no nulos en \(\mathbb{R}^2\), llamados \(\mathbf{v}_1=(2,1)\) y \(\mathbf{v}_2=(1,2)\). Vamos a estudiar el conjunto de todas las combinaciones lineales de estos dos vectores. Para ello vamos a graficar los vectores \(\mathbf{v}_1\) y \(\mathbf{v}_2\) y luego multiplicamos a estos vectores por dos números reales \(c_1\) y \(c_2\) y graficamos el vector resultante. Como lo vemos en la siguiente figura el conjunto de todas las combinaciones lineales de \(\mathbf{v}_1\) y \(\mathbf{v}_2\) es un plano de color
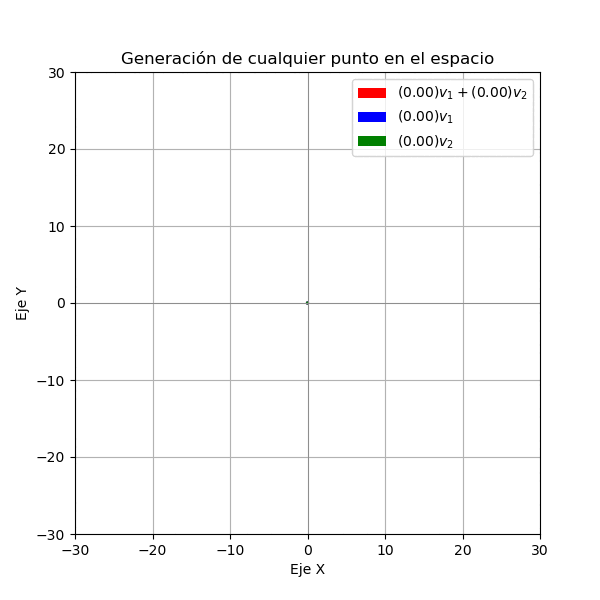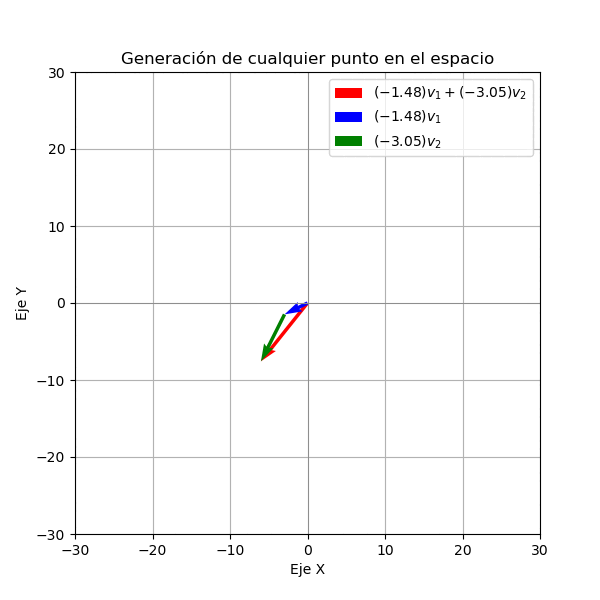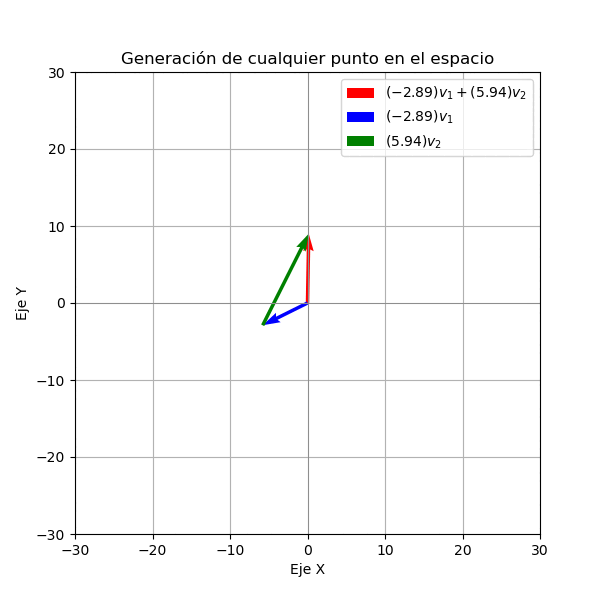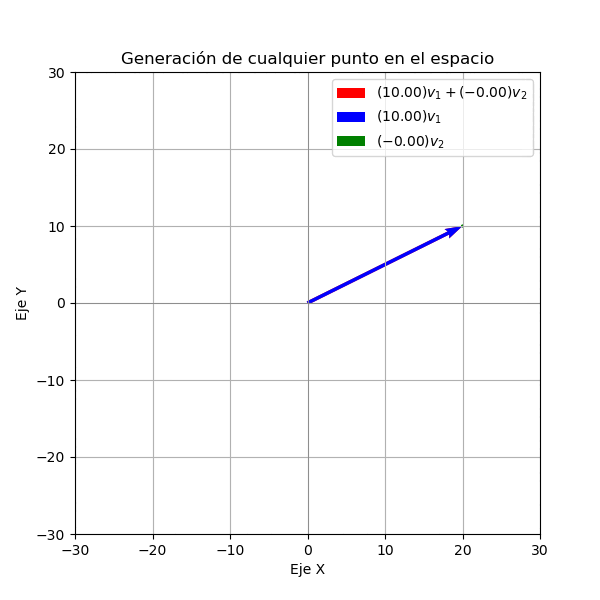
Note que en este caso podemos ver que el espacio generado por todos los vectores es \(\mathbb{R}^2\).
Definición: Un conjunto de vectores \(W=\{\mathbf{v}_1,\mathbf{v}_2,\ldots,\mathbf{v}_n\}\) en \(\mathbb{R}^n\) es linealmente independiente si la única combinación lineal de los vectores de \(W\) que da como resultado el vector cero es la combinación lineal trivial, es decir, si
\[\alpha_1 \mathbf{v}_1 + \alpha_2 \mathbf{v}_2 + \ldots + \alpha_n \mathbf{v}_n = \mathbf{0}\]
entonces \(\alpha_1 = \alpha_2 = \ldots = \alpha_n = 0\). Si un conjunto de vectores no es linealmente independiente, se dice que es linealmente dependiente.
Ejemplo
Note que los vectores \(\mathbf{v}_1=(1,1)\) y \(\mathbf{v}_2=(-1,1)\) son linealmente independientes, ya que la única combinación lineal de estos vectores que da como resultado el vector cero es la combinación lineal trivial. Es decir, si \(\alpha_1 \mathbf{v}_1 + \alpha_2 \mathbf{v}_2 = \mathbf{0}\), entonces \(\alpha_1 = \alpha_2 = 0\). ¿Por qué?
Definición
Un conjunto de vectores \(W=\{\mathbf{v}_1,\mathbf{v}_2,\ldots,\mathbf{v}_n\}\) en \(\mathbb{R}^2\) es una base si cumple las siguientes dos condiciones:
- Los elementos de \(W\) son linealmente independientes.
- \(Span(W)=\mathbb{R}^2\). Es decir, cualquier vector en \(\mathbb{R}^2\) se puede expresar como una combinación lineal de los vectores de \(W\).