No artists with labels found to put in legend. Note that artists whose label start with an underscore are ignored when legend() is called with no argument.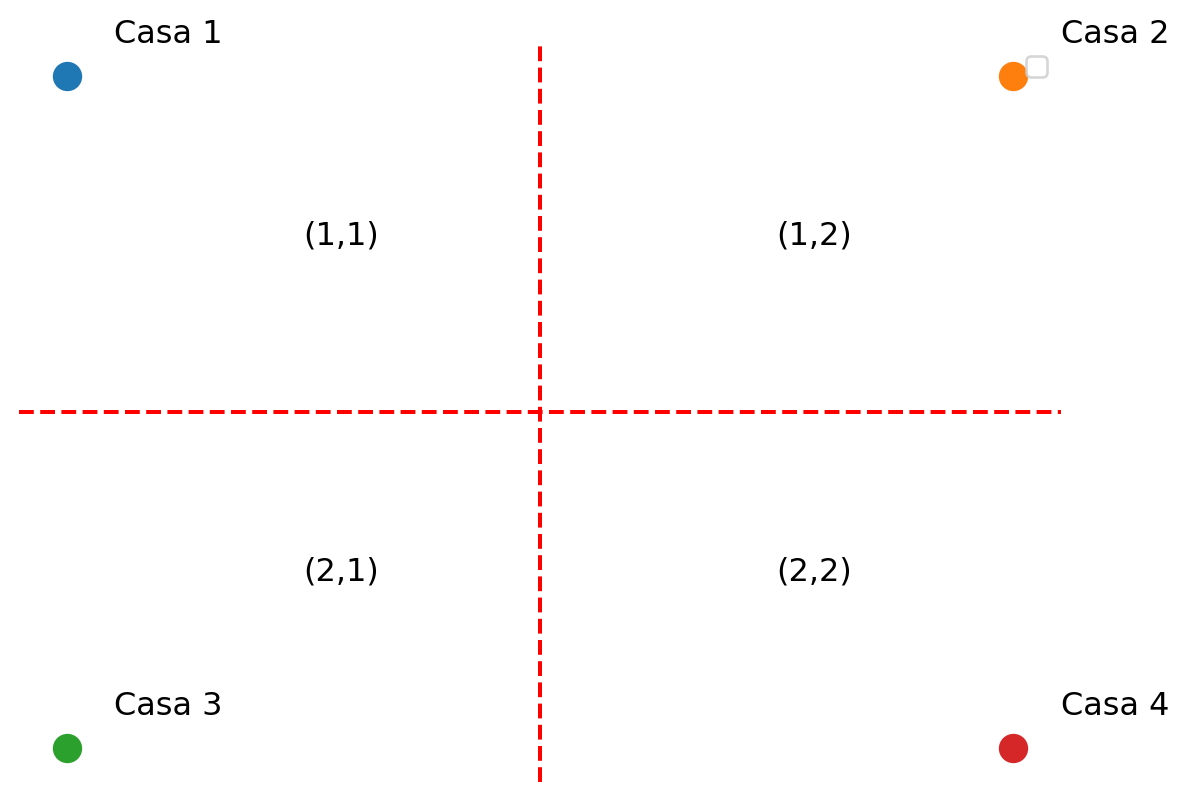
Matrices
Supongamos que tenemos una ciudad solo con 4 casas, podemos colocar una nomenclatura para cada una de la casa usando solo números de la siguiente forma:
Note que en la casa 1 la dirección sería (1,1), en la casa 2 la dirección sería (1,2), en la casa 3 la dirección sería (2,1) y en la casa 4 la dirección sería (2,2). De esta forma podemos decir encontrar que esta “viviendo” en cada casa. Podemos suponer que en la casa 1 vive el número 1, en la casa 2 el número 2 y así sucesivamente. Para representar esto podemos usar una notación matricial de la siguiente forma:
\[ A=\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix} \]
De esta forma podemos definir que en la dirección \((1,1)\) esta viviendo el número 1, esto lo podemos representar de la forma
\[A(1,1)=1,\]
similarmente
\[A(1,2)=2, \ A(2,1)=3 \text{ y } A(2,2)=4\]
El elememto \(A\) se llama una matriz, cuya dimensión es \(2\times 2\) que representan las casas de la ciudad. Llamaremos filas de la matriz \(A\) a los elementos que están en la misma fila y columnas a los elementos que están en la misma columna. Por ejemplo la fila 1 de la matriz \(A\) es \((1,2)\) y la columna 1 de la matriz \(A\) es \(\begin{bmatrix}1\\3\end{bmatrix}\).
Operaciones con matrices
Suma de matrices
Para sumar dos matrixces \(A\) y \(B\) de la misma dimensión, se suman los elementos correspondientes de cada matriz. Por ejemplo, si tenemos dos matrices \(A\) y \(B\) de dimensión \(2\times 2\):
\[ A=\begin{bmatrix}1 & 2\\3 & 4\end{bmatrix} \text{ y } B=\begin{bmatrix}5 & 6\\7 & 8\end{bmatrix}\]
La suma de estas dos matrices sería:
\[ A+B=\begin{bmatrix}1+5 & 2+6\\3+7 & 4+8\end{bmatrix}=\begin{bmatrix}6 & 8\\10 & 12\end{bmatrix}\]
Multiplicación por escalar
La multiplicación de una matriz por un escalar \(\alpha\) (recuerda que un número escalar es un real) se realiza multiplicando cada elemento de la matriz por el escalar. Por ejemplo, si tenemos una matriz \(A\) de dimensión \(2\times 2\):
\[ A=\begin{bmatrix}1 & 2\\3 & 4\end{bmatrix}\]
y multiplicamos la matriz \(A\) por el escalar \(\alpha=2\):
\[ 2A=\begin{bmatrix}2 & 4\\6 & 8\end{bmatrix}\]
Multiplicación de matrices
La multiplicación de matrices es un poco más complicada que la suma de matrices. Para multiplicar dos matrices \(A\) y \(B\) se debe cumplir que el número de columnas de la matriz \(A\) sea igual al número de filas de la matriz \(B\). Por ejemplo, si tenemos dos matrices \(A\) y \(B\) de dimensión \(2\times 2\):
\[ A=\begin{bmatrix}1 & 2\\3 & 4\end{bmatrix} \text{ y } B=\begin{bmatrix}5 & 6\\7 & 8\end{bmatrix}\]
La multiplicación de estas dos matrices sería:
\[ AB=\begin{bmatrix}1\cdot 5+2\cdot 7 & 1\cdot 6+2\cdot 8\\3\cdot 5+4\cdot 7 & 3\cdot 6+4\cdot 8\end{bmatrix}=\begin{bmatrix}19 & 22\\43 & 50\end{bmatrix}\]
Ahora notemos que la multiplicación no es conmutativa, es decir, en general \(AB\neq BA\).
\[ BA=\begin{bmatrix}5\cdot 1+6\cdot 3 & 5\cdot 2+6\cdot 4\\7\cdot 1+8\cdot 3 & 7\cdot 2+8\cdot 4\end{bmatrix}=\begin{bmatrix}23 & 34\\31 & 46\end{bmatrix}\]
Sea \(X=\begin{bmatrix}1 \\ 2\end{bmatrix}\) un vector columna, note que su diemnsión es \(2\times 1\). Si multiplicamos la matriz \(A\) por el vector \(X\):
\[ AX=\begin{bmatrix}1\cdot 1+2\cdot 2\\3\cdot 1+4\cdot 2\end{bmatrix}=\begin{bmatrix}5\\11\end{bmatrix}\]
Note que la multiplicación de la \(XA\) no esta definida ya que el número de columnas de la matriz \(X\) no es igual al número de filas de la matriz \(A\).
De la misma forma podemos ver el vector fila \(Y=\begin{bmatrix}1 & 2\end{bmatrix}\), que su dimensión es \(1\times 2\). Si multiplicamos la matriz \(A\) por el vector \(YA\) así:
\[ YA=\begin{bmatrix}1\cdot 1+2\cdot 3 & 1\cdot 2+2\cdot 4\end{bmatrix}=\begin{bmatrix}7 & 10\end{bmatrix}\]
Note que la multiplicación de la \(AY\) no esta definida ya que el número de columnas de la matriz \(A\) no es igual al número de filas de la matriz \(Y\). ## Transpuesta de una matriz
La transpuesta de una matriz \(A\) se denota por \(A^T\) y se obtiene intercambiando las filas por las columnas. Por ejemplo, si tenemos una matriz \(A\) de dimensión \(2\times 3\):
\[ A=\begin{bmatrix}1 & 2 & 3\\4 & 5 & 6\end{bmatrix}\]
La transpuesta de la matriz \(A\) sería:
\[ A^T=\begin{bmatrix}1 & 4\\2 & 5\\3 & 6\end{bmatrix}\]
Matriz identidad
La matriz identidad es una matriz cuadrada cuyos elementos de la diagonal principal son 1 y los demás elementos son 0. La matriz identidad de dimensión \(n\) se denota por \(I_n\). Por ejemplo, la matriz identidad de dimensión \(2\) es:
\[ I_2=\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}\]
Inversa de una matriz
La inversa de una matriz \(A\) se denota por \(A^{-1}\) y se define únicamente para una matriz cuadrada, como la matriz que al multiplicarla por la matriz \(A\) nos da la matriz identidad. Es decir, si \(A\) es una matriz cuadrada, entonces \(A^{-1}\) es la matriz tal que:
\[ A\cdot A^{-1}=I\]
y
\[ A^{-1}\cdot A=I\]
Note únicamente en este caso se tiene que \(A^{-1}\cdot A=A\cdot A^{-1}\).
Cuando tenemos una matriz de \(2\times 2\) existe una formula para calcular la inversa de una matriz y esta determinada por
La inversa de la matriz \(A\) sería:
Si \(A=\begin{bmatrix}a & b\\c & d\end{bmatrix}\), entonces la inversa de la matriz \(A\) se define como:
\[ A^{-1}=\frac{1}{ad-bc}\begin{bmatrix}d & -b\\-c & a\end{bmatrix}\]
donde \(a\), \(b\), \(c\) y \(d\) son los elementos de la matriz \(A\).
Ejemplo si tenemos la matriz \(A=\begin{bmatrix}1 & 2\\3 & 4\end{bmatrix}\), entonces la inversa de la matriz \(A\) sería:
\[ A^{-1}=\frac{1}{1\cdot 4-2\cdot 3}\begin{bmatrix}4 & -2\\-3 & 1\end{bmatrix}=\frac{1}{-2}\begin{bmatrix}4 & -2\\-3 & 1\end{bmatrix}=\begin{bmatrix}-2 & 1.\\1.5 & -0.5\end{bmatrix}\]